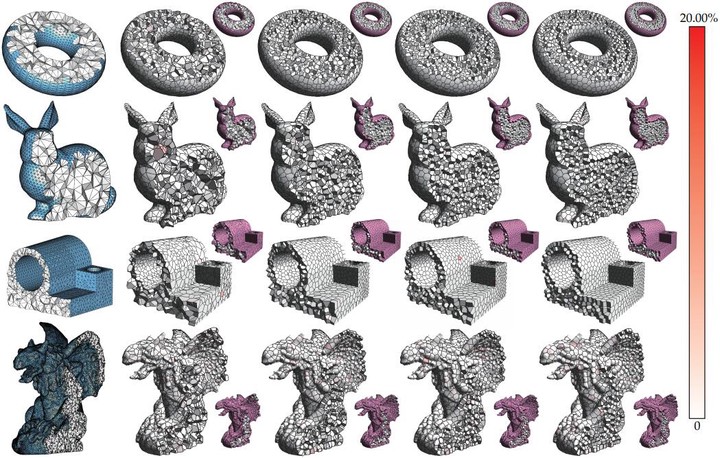
 Results of Lloyd’s iterations using our method.
Results of Lloyd’s iterations using our method.
Abstract
Computing the Voronoi diagram of a given set of points in a restricted domain (e.g. inside a 2D polygon, on a 3D surface, or within a volume) has many applications. Although existing algorithms can compute 2D and surface Voronoi diagrams in parallel on graphics hardware, computing clipped Voronoi diagrams within volumes remains a challenge. This study proposes an efficient GPU algorithm to tackle this problem. A preprocessing step discretizes the input volume into a tetrahedral mesh. Then, unlike existing approaches which use the bisecting planes of the Voronoi cells to clip the tetrahedra, we use the four planes of each tetrahedron to clip the Voronoi cells. This strategy drastically simplifies the computation, and as a result, it outperforms state-of-the-art CPU methods up to an order of magnitude.